目标
本篇主要介绍了以下几点:
- 了解图像噪声,何为图像中的噪声。
- 何为加性均值高斯噪声。加性为什么意思?均值又表示了什么?高斯噪声有何特点?
- 如何产生加性零均值高斯噪声。如何产生正太分布?Box-Muller变换又是什么?
- 如何编程实现?
噪声
实际的图像经常会受到一些随机的影响而退化,可以理解为原图受到干扰和污染。通常就就把这个退化成为噪声(noise)。在我们采集、传输或者处理的过程中都有可能产生噪声,因此噪声的出现是多方面的原因。
在信号处理中我们用概率特征来描述噪声,即噪声出现的概率呈现为什么样子就为什么样子的噪声。就比如本篇的主角高斯噪声,其在信号中出现、分布的概率成高斯分布(正态分布)。也许你会疑问噪声概率分布应是无规律的,现实中也确实噪声严格上是不规律的分布,但是为了简化计算,人们常将噪声理想化,这种理想型的概率分布模型来描述的噪声称为白噪声。白噪声在信号中是典型的,其特点是具有常量功率谱。而高斯噪声属于白噪声的一个特例。
加性零均值高斯噪声
加性噪声的表示为以下表达式
$$
f(x, y) = g(x, y) + v(x,y)
$$
g为原图像信号,v为噪声信号,两者关系是独立的,这表示原图信号如何变化与噪声无光,噪声不依赖于图像信号,这种独立与信号的噪声便称为加性噪声(additive noise)。
均值为零,即噪声为高斯分布,高斯分公式中的均值为0,即高斯分布的对称轴为0。
产生原理步骤
(1)假定图像的灰阶范围是【0,G-1】。取$\sigma > 0$;它的值很小时,相应的噪声也小。
(2)针对每个水平相邻的像素$(x,y),(x,y+1)$产生一对位于【0,1】范围内的独立随机数 $\gamma, \phi$。
(3)计算
$$z_1 = \sigma cos(2\pi\phi)\sqrt{-2\ln\gamma}$$
$$z_2 = \sigma cos(2\pi\phi)\sqrt{-2\ln\gamma}$$
(4)置$f^,(x,y) = g(x,y) + z_1$ 和 $f^,(x,y + 1) = g(x,y+1) + z_2$,其中$g$是输入图像。
(5)置
$$f(x,y)=\begin{cases} 0 &{当f^,(x,y) < 0} \G-1 &{当f^,(x,y) > G-1} \f^,(x,y) &\text{其他} \end{cases}$$
$$f(x,y+1)=\begin{cases}0 &{当f^,(x,y+1) < 0}\G-1 &{当f^,(x,y+1) > G-1}\f^,(x,y+1) &\text{其他}\end{cases}$$
(6)跳转到步骤3,直到扫描完所有的像素。
何为Box-Muller变换,简单的说通过服从均匀分布的随机变量,来构建服从高斯分布的随机变量的一种方法。推导过程可以阅读知乎的这篇博文Box-Muller变换原理详解
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
#pragma once
// Copyright https://mangoroom.cn
// License(MIT)
// Author:mango
// gaussian_noise | 高斯噪声
// this is gaussian_noise.h
#include<opencv2/opencv.hpp>
namespace imageprocess
{
void GaussionNoise(cv::Mat & image);
}//namespace imageproccess
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
// Copyright https://mangoroom.cn
// License(MIT)
// Author:mango
// gaussian_noise | 高斯噪声
// this is gaussian_noise.cpp
#include"gaussian_noise.h"
#include<cmath>
#include<random>
#include<ctime>
void imageprocess::GaussionNoise(cv::Mat & image)
{
// step1: Check the input paramter :检出输入参数
assert(!image.empty());
assert(3 == image.channels()); // only color image
// step2: Initialize the value of sigma :初始化sigma值
double sigma = 1;
// step3: Initialize 2 random numbers gamma、phi for every pixel: 针对初始化2两个随机数gamma、phi
std::default_random_engine random(time(NULL));
std::uniform_real_distribution<double> dis(0, std::nextafter(1, DBL_MAX));
for (size_t i = 0; i < image.rows - 1; i++)
{
for (size_t j = 0; j < image.cols; j++)
{
double gamma = dis(random);
double phi = dis(random);
// step4: Compute the normal distribution by Box-Muller transfer:通过Box-Muller变换求解正态分布
double z1 = sigma * std::cos(2 * 3.1415 * phi) * std::sqrt(-2 * log(gamma));
double z2 = sigma * std::sin(2 * 3.1415 * phi) * std::sqrt(-2 * log(gamma));
// step5: Add the gaussion noise to pixels: 添加噪声到像素点
for (size_t k = 0; k < 3; k++)
{
double f1 = image.at<cv::Vec3b>(i, j)[k] + z1;
double f2 = image.at<cv::Vec3b>(i + 1, j)[k] + z2;
image.at<cv::Vec3b>(i, j)[k] = cv::saturate_cast<uchar>(f1);
image.at<cv::Vec3b>(i + 1, j)[k] = cv::saturate_cast<uchar>(f2);
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// Copyright https://mangoroom.cn
// License(MIT)
// Author:mango
// image proccess algorithm | 图像处理算法
// this is main.cpp
#include"gaussian_noise.h"
int main()
{
//cv::Mat src = cv::Mat(cv::Size(500, 300), CV_8UC3, cv::Scalar(200,200,200));
cv::Mat src = cv::imread("./images/lena.jpg");
imageprocess::GaussionNoise(src);
cv::imshow("sigma=1", src);
cv::waitKey(0);
return 0;
}
|
运行结果
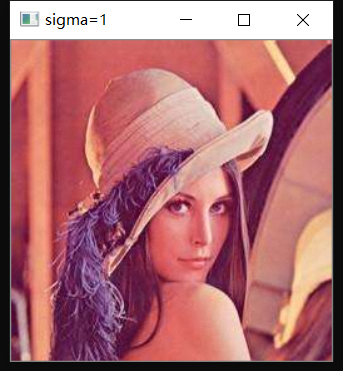
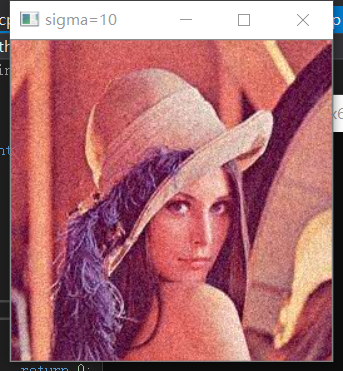

reference
【1】图像处理、分析与机器视觉4th
【2】Box-Muller变换原理详解-知乎
本文由芒果浩明发布,转载请注明来源。
本文链接:https://blog.mangoeffect.net/opencv/create-additive-zero-mean-gaussion-noise.html




