简介
本文主要介绍了大津法的算法原理，而后python与c++编码实现算法进行实验。
算法原理
设T为前景和背景的分割阈值，按阈值T分割后得到前景和背景。前景像素点占比为$w_f$, 平均灰度为$u_f$,相应的背景像素占比为$w_b$,平均灰度为$u_b$。则可以求得总灰度平均为
$$u = w_f \times u_f + w_b \times u_b \tag{1}$$
类间方差为
$$\sigma^2 = w_f \times(u_f -u)^2 + w_b \times(u_b - u)^2 \tag{2}$$
将1式带入2式可得
$$\sigma^2 = w_f \times w_b (u_f - u_b)^2 \tag{3}$$
式的结果类间方差是在分割阈值为T的时候求得的，改变阈值T的时候,前景背景的像素占比和平均灰度将会改变，结果类间方差也会随之改变，因此类间方差是关于分割阈值的函数
$$\sigma^2(t) = w_f \times w_b (u_f - u_b)^2 \tag{3}$$
而$w_f, w_b, u_b,u_f$是关于分割阈值T的函数
$$\begin{cases} w_f = f_1(t) \w_b = f_2(t) \u_f = f_3(t) \u_f = f_4(t)\end{cases}$$
而大津法又名最大类间方差法，即求解是类间方差$\sigma^2$取得最大值的分割阈值T,此时分割阈值就被认为是最合适的二值化阈值。
大津法按图像的灰度特性,将图像分成背景和前景两部分。因方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。
实验
以一张经典的lena图为例
通过计算可以得到此图的类间方差曲线是这样的
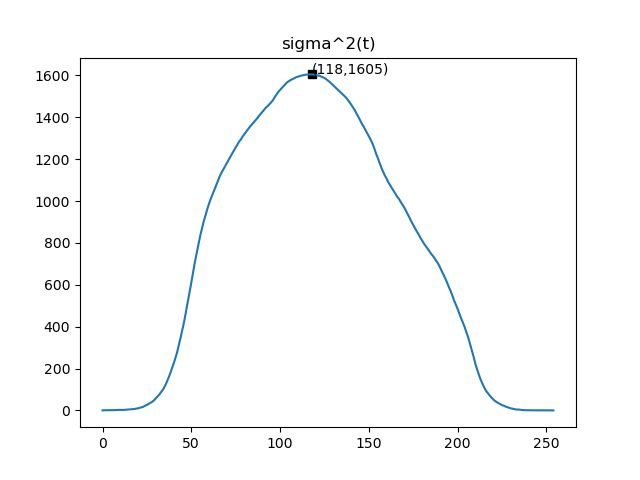找到最大值点，横坐标便是最佳的分割阈值，可以在直方图中标记出分割阈值
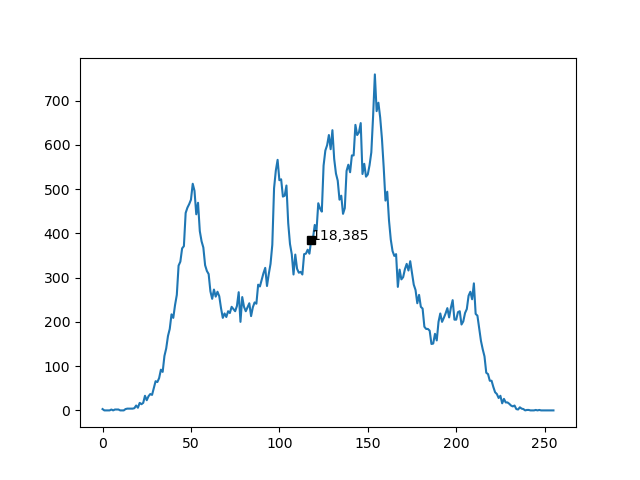最后，用此阈值分割结果如下
再来看看以文本图为实验的效果
类间方差曲线
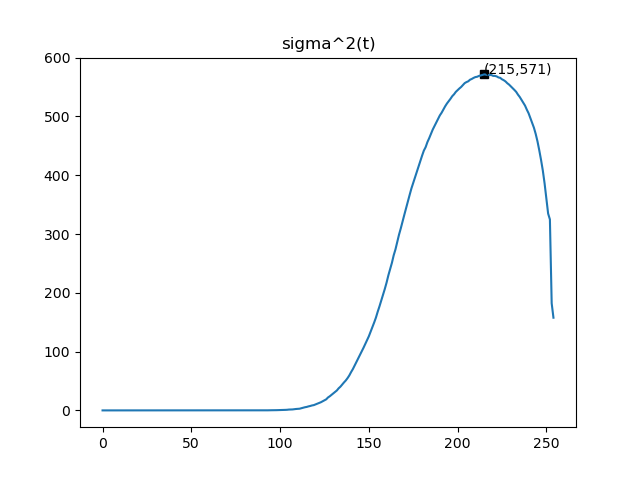最佳阈值
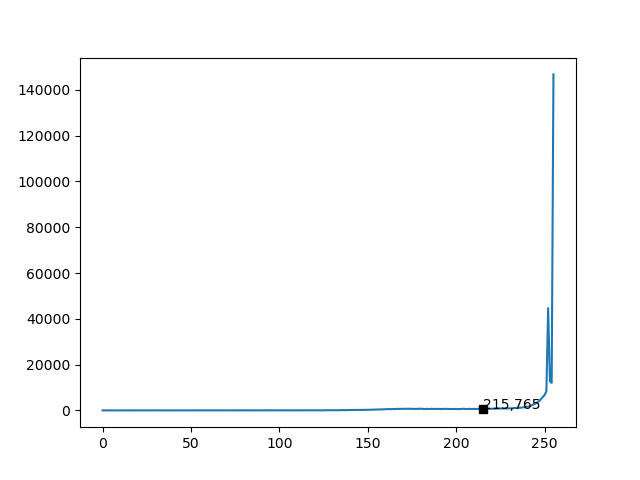分割结果
代码
python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
#/usr/bin/env python
"this is a otsu test case"
import cv2
from matplotlib import pyplot as plt
import numpy as np
def histogram(img):
rows = img.shape[0]
cols = img.shape[1]
htg = [ 0 for i in range(256)]
for r in range(rows):
for c in range(cols):
v = img[r][c]
htg[v] += 1
return htg
def calcCdf(histogram, pixelCount):
cdf = [0 for i in range(256)]
cdf[0] = histogram[0] / pixelCount
for i in range(1, 256):
cdf[i] = cdf[i-1] + histogram[i] / pixelCount
return cdf
def otsu(image):
htg = histogram(image)
pixelCount = image.shape[0] * image.shape[1]
cdf = calcCdf(htg,pixelCount)
sigma = [0 for i in range(255)]
for t in range(1, 255):
w_b = cdf[t]
w_f = 1 - w_b
# backgroud pixels grayscale sum
sum_b = 0
p1 = 0
for i in range(t):
sum_b += i * htg[i]
p1 += htg[i]
# foregroud pixels grayscale sum
p2 = 0
sum_f = 0
for j in range(t, 256):
sum_f += j * htg[j]
p2 += htg[j]
if p1 == 0 or p2 == 0:
continue
u_b = sum_b / p1
u_f = sum_f / p2
sigma[t] = w_f * w_b * ((u_f - u_b)**2)
return sigma
if __name__ == '__main__':
image = cv2.imread("text.png", 0)
htg = histogram(image)
htg2 = cv2.calcHist([image], [0], None, [256], [0.0, 255.0])
sigma = otsu(image)
t = sigma.index(max(sigma))
#plt.plot(htg)
#showT = str(int(t)) + "," + str(int(htg[t]))
#plt.plot(t, htg[t], 'ks')
#plt.annotate(showT, xy = (t, htg[t]))
plt.plot(sigma.index(max(sigma)), max(sigma), 'ks')
showMax = "(" + str(int(sigma.index(max(sigma)))) + "," + str(int(max(sigma))) + ")"
plt.annotate(showMax, xy=(sigma.index(max(sigma)), max(sigma)))
plt.plot(sigma)
plt.title('sigma^2(t)')
(T, dst) = cv2.threshold(image, t, 255,cv2.THRESH_BINARY)
(T2,dst2) = cv2.threshold(image,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
print(T2)
cv2.imshow("otsu",dst)
#cv2.imshow("otsu-by-opencv", dst2)
cv2.waitKey(0)
plt.show()
|
c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
#pragma once
#include<opencv2/core.hpp>
#include<cassert>
#include<algorithm>
// gray histogram
void GrayHistogram(const cv::Mat& gray_image, std::array<int, 256>& histogram)
{
// check the input parameter : 检查输入参数
assert(gray_image.channels() == 1);
assert(histogram.size() == 256);
// step1: All elements of the histogram array are assigned a value of 0 : 将数组histogram所有的元素赋值为0
histogram = { 0 };
// step2: Do hf[f(x,y)]+1 for all pixels of the image: 对图像所有元素，做hf[f(x,y)]+1
for (size_t i = 0; i < gray_image.rows; i++)
{
for (size_t j = 0; j < gray_image.cols; j++)
{
int z = gray_image.at<uchar>(i, j);
histogram.at(z) += 1;
}
}
}
unsigned int Otsu(const cv::Mat& image)
{
assert(image.channels() == 1);
int maxT = 1; //threshold
int maxSigma = 0;
std::array<int, 256> histogram = { 0 };
std::array<float, 256> cdf = { 0.0f };
GrayHistogram(image, histogram);
int pixelAll = image.rows * image.cols;
int pixelSum = 0;
for (size_t i = 0; i < 256; i++)
{
pixelSum += histogram[i];
cdf[i] = static_cast<float>(pixelSum) / pixelAll;
}
std::array<int, 256> sigma{ 0 };
for (size_t t = 1; t < 255; t++)
{
float w_b = cdf[t];
float w_f = 1 - w_b;
int p1 = 0;
int sum_b = 0;
for (int i = 0; i < t; ++i)
{
sum_b += i * histogram[i];
p1 += histogram[i];
}
int sum_f = 0;
int p2 = 0;
for (int j = t; j < 256; j++)
{
sum_f += j * histogram[j];
p2 += histogram[j];
}
if(0 == p1 || 0 == p2)
{
continue;
}
int u_b = sum_b / p1;
int u_f = sum_f / p2;
sigma[t] = w_f * w_b * (u_b - u_f) * (u_b - u_f);
}
auto it = max_element(sigma.begin(), sigma.end());
return static_cast<unsigned int>(std::distance(sigma.begin(), it));
};
|
本文由芒果浩明发布，转载请注明出处。
本文链接：https://blog.mangoeffect.net/opencv/otsu-image-binary.html
