序
这个问题源于知乎上的一个问题,起初也是按照自己的理解尝试着答了以下。但或许问题没多少人关注,截至目前(2019.06.05)为止,总回答数量仅有5个。芒果便将之前的答案整理一下作为记录。
问题理解
卷积是一种运算操作,傅里叶变换是一种变换操作。卷积在图像处理的应用中一个重要作用是卷积滤波,即用一个卷积模板(卷积核/滤波器)去对图像进行滤波。而傅里叶变换在信号处理中往往是变换时域和频域,在图像处理中则是变换空域和频域。那么我先把你说的边缘处理就认为是图像滤波里面的一种好了。如此一来,那问题就理解为是图像处理空域滤波和时域滤波的对比了。即问题的的关键就是要搞懂为什么如今的图像滤波处理大多采用空域滤波而非频域滤波。
空域卷积滤波
首先,先看一下空域滤波,现如今图像处理的空域滤波大多为卷积滤波或者相关滤波,但两者原理相似。理解卷积滤波即可明白原因所在。卷积滤波的基本原理可以简单理解为用一个卷积核与整幅图像进行卷积运算操作,有关卷积更详细的理解可以参考这篇博文c++实现二维卷积。这里附上代码实现
|
|
按照卷积运算,可以计算算法的复杂度。
卷积算法复杂度
可以得到,假如原图是MxN大小,卷积核为m*n, 时间复杂度约为M x N x m x n 而卷积核通常比较小,一般有 3 x 3 和 5 x 5等,所以可以卷积滤波算法复杂度可以约为c x M x N ,c为常数
频域傅里叶变换滤波
频域域滤波过程与一般信号处理一样,就是傅里叶变换到时域->在时域进行操作->傅里叶反变换回空域。
- 原图像大小 M * N
- 扩充后, 2M * 2 N
- fft变换到频域, 计算量 2M * 2N * log( 2M * 2N), 即 4M * N * log (4M * N)
- 对应相乘, 计算量 2M * 2N ,即4M * N
- ifft变换回空域, 计算量 2M * 2N * log( 2M * 2N), 即 4M * N * log (4M * N)
- 所以可以得到频域滤波算法复杂度为4M*N + 4M * N * log (4M * N)
即M*N(4 + log(4M * N))。 所以与 c * M * N 相比,算法复杂度上频域滤波一般是没什么优势的。
引入高频分量
然后另一个点是,在频域滤波第2(扩充图像)步中,扩充图像回引入高频分量,从而带来干扰。
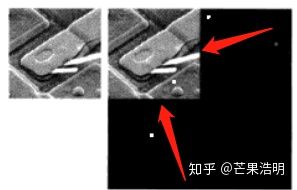 如图,扩充后,两个边界就会引入高频分量。
如图,扩充后,两个边界就会引入高频分量。
两个主要原因
所以芒果认为,一是算法复杂度没有相比卷积没有优势,二是可能会引入高频分量干扰。卷积的方法会更适合在实际应用的处理之中,而傅里叶变换到频域去我觉得更适合用来分析就好。
其他回答
- 甜草莓
|
|
- 斯温
|
|
尾巴
以上是芒果对此问题的一些理解,可能不太全面,但应该是原因之一。或许还可能是因为编程的难易程度不同,使得卷积滤波相比傅里叶变换更受欢迎。
本文由芒果浩明发布,转载需注明来源。 本文链接:https://blog.mangoeffect.net/algorithm/why-convolution-not-fft.html
